Tangent Fitting

In this chapter, we will develop a methodology to fit empirical models to the maximum intensity arc of the image, under the assumption that the tangent hypothesis holds true. As we saw in Extracting the magnetopause surface from the simulation, this depends strongly on the orbit and corresponding viewing angles of the satellite. We suppose here that this method will be utilized under the conditions dictated by the hypothesis and its limits. In this subset of cases, complete characterization of the method, shall also take into account the error propagation of the tangent hypothesis.

When trying to extract 3D information from a 2D image, we need to make some assumptions to account for the loss of information from the integration over the third axis. In the tangent fitting approach we attempt to reconstruct this information by assuming a particular shape for the magnetopause - an empirical model. A first approach could be, to trace the maximum intensity arc and then try to fit the model parameters to the arc, for that particular POV. However, we already saw in Image processing that extracting a clean curve that follows the intended shape is not a simple extraction of the maximum intensity per row. Quite a few filters, as well as limits of steps were introduced to improve the detection, while the extraction still fails in certain viewing angles. We should also remember that the images that we are analyzing do not include any instrumental noise, background contributions or binning of the resolution. A more realistic image of what we expect the instrument to see, including background contribution, instrumental noise and resolution, is shown in Fig. 12. The SXI team has developed the relevant tools, not only to simulate the expected noise and background, but also to subtract it from the final images and aid in their processing.

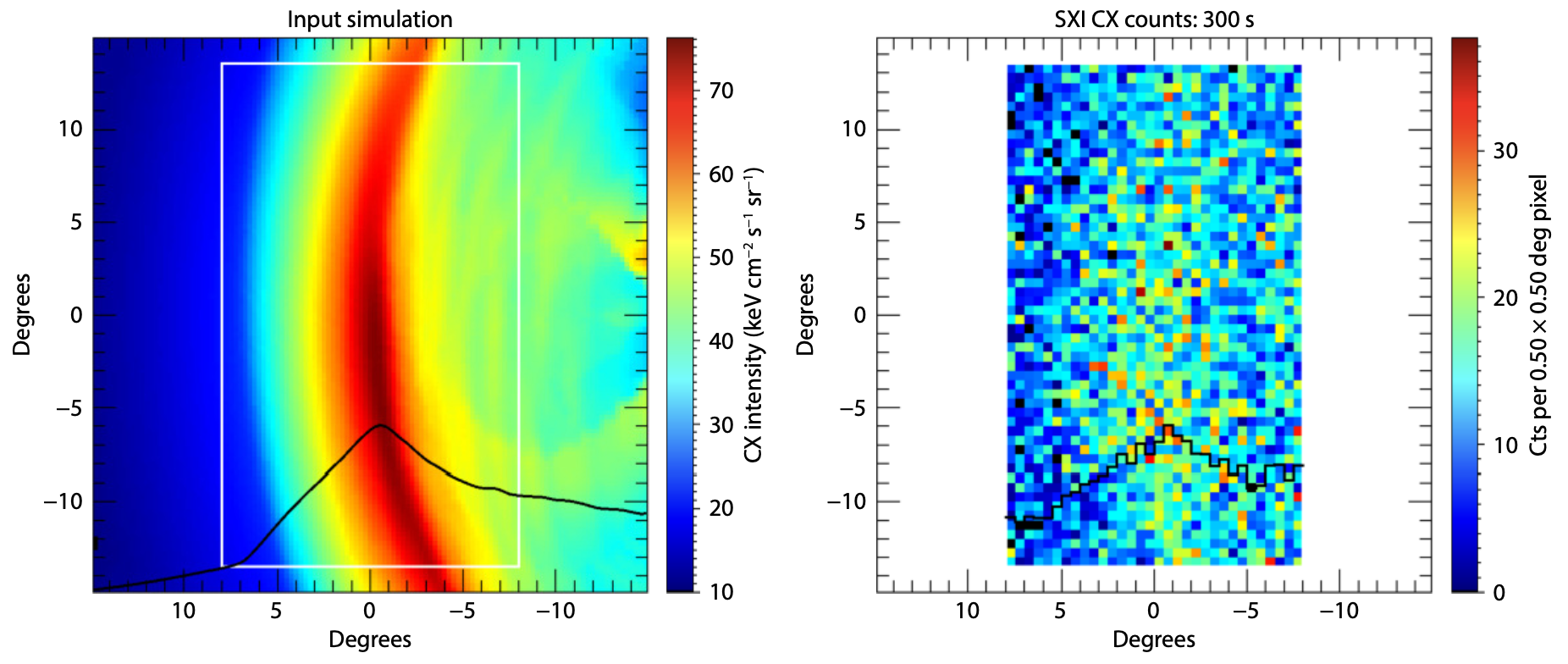
Fig. 12 Input image constructed from MHD simulations and output image of the SXI noise and background simulator. [Sembay et al., 2024]

This is also the case for a MHD image, meaning that the details introduced by the test particles will make detection even more difficult. Therefore, a different methodology was developed in order to address this problem and return the best fitted parameters of the empirical model simultaneously.